![An Australian Government Initiative [logo]](/images/austgovt_brown_90px.gif)


![An Australian Government Initiative [logo]](/images/austgovt_brown_90px.gif) |
 |
 |

This section will illustrate a number of the macroscopic features that have been used in fungal classification or identification. The list is certainly not comprehensive, but you will get a good idea of the range of features. So, the next time you see a mushroom, polypore, puffball or whatever, you may look at it with new eyes and see features you hadn’t thought of before – and you’ll undoubtedly see features that aren’t mentioned here.
There are technical names for many of the things described below but, for the
most part, the technical terms are omitted. They are not essential here for
the aim is simply to familiarise you with the nature (not the jargon) of many
identification features. ![]() You
can find the technical terms in many fungal books, such as the references given
here.
You
can find the technical terms in many fungal books, such as the references given
here.
Through the 1800s and into the early 1900s, fungal classification relied heavily on the macroscopic features of the fruiting body, though the late 1800s saw increasing attention given to microscopic features. In the 1900s the microscopic features became more important so, while all of the features mentioned below are still very useful for identification, their role in classification is often much reduced.
Of prime importance is the type of fruiting body (e.g. mushroom, puffball, cup fungus, polypore, etc (SEE TYPES OF FUNGI SECTION).
 Even
within any single type of fruiting body there may be much variation in shape.
For example, while all mushrooms have gills under their caps - mushrooms come
in many shapes and sizes. The caps may be steeply conical, hemispherical, slightly
convex, flat, flat with a central hump (a bit like a sombrero) or funnel shaped.
The stems may be cylindrical, narrower at the top, narrower at the bottom, bowing
in the middle, cylindrical except for a swollen ball-like base - or there's
no stem at all and the cap simply grows out of a piece of wood. The caps may
be just a few millimetres in diameter or many centimetres in diameter and the
stems may be solid or hollow inside. The accompanying diagram shows some of
the possibilities.
Even
within any single type of fruiting body there may be much variation in shape.
For example, while all mushrooms have gills under their caps - mushrooms come
in many shapes and sizes. The caps may be steeply conical, hemispherical, slightly
convex, flat, flat with a central hump (a bit like a sombrero) or funnel shaped.
The stems may be cylindrical, narrower at the top, narrower at the bottom, bowing
in the middle, cylindrical except for a swollen ball-like base - or there's
no stem at all and the cap simply grows out of a piece of wood. The caps may
be just a few millimetres in diameter or many centimetres in diameter and the
stems may be solid or hollow inside. The accompanying diagram shows some of
the possibilities.
Sometimes you will need to look at both young and old specimens. The young mushrooms of Cortinarius archeri ![]() are a striking purple but they become brownish when older. These young Inkcap mushrooms
are a striking purple but they become brownish when older. These young Inkcap mushrooms ![]() , growing on a rotting hay bale, have noticeably shaggy caps but in these older caps
, growing on a rotting hay bale, have noticeably shaggy caps but in these older caps ![]() the shagginess has begun to disappear and soon there would be no trace left. I'll finish with three views of a species of Psathyrella - the very young mushrooms
the shagginess has begun to disappear and soon there would be no trace left. I'll finish with three views of a species of Psathyrella - the very young mushrooms ![]() only two to three millimetres tall, an older specimen
only two to three millimetres tall, an older specimen ![]() with the stem about a centimetre long and four mature specimens,
with the stem about a centimetre long and four mature specimens, ![]() the caps about two centimetres in diameter.
the caps about two centimetres in diameter.
These photos show species of Crepidotus ![]() and Resupinatus
and Resupinatus ![]() .
Both grow on dead wood and neither has a stem. In the former the cap is attached
at it’s edge and in the latter the cap is attached by its top. The fruiting
bodies of Campanella, like those of Resupinatus, are stem-less
mushrooms that typically grow on the underside of dead wood lying on the ground.
however, while Resupinatus has fairly standard gills, radiating from
the point where the cap is attached tot he wood, Campanella is different.
Here are two specimens, one brown
.
Both grow on dead wood and neither has a stem. In the former the cap is attached
at it’s edge and in the latter the cap is attached by its top. The fruiting
bodies of Campanella, like those of Resupinatus, are stem-less
mushrooms that typically grow on the underside of dead wood lying on the ground.
however, while Resupinatus has fairly standard gills, radiating from
the point where the cap is attached tot he wood, Campanella is different.
Here are two specimens, one brown ![]() and the other white
and the other white ![]() ,
both collected on Norfolk Island. While each has a few radial gills, there are
also numerous cross-connections between the gills.
,
both collected on Norfolk Island. While each has a few radial gills, there are
also numerous cross-connections between the gills.
Some mushrooms have a skirt of tissue (called a ring or annulus)
around the stem, as shown in this picture of an Agaricus species ![]() .
Another feature possessed by some mushrooms is a cup-like structure (or volva)
around the base of the stem, as shown in this photo of a species of Amanita
.
Another feature possessed by some mushrooms is a cup-like structure (or volva)
around the base of the stem, as shown in this photo of a species of Amanita
![]() .
Most mushroom genera have neither a ring nor a volva (with a volva being rarer
than a ring). Thus the possession of one (or both) of these features is of great
help in identification. Volva and ring are remnants of tissues that are present in the young stages of many mushrooms. A universal veil is a membrane that envelops the whole of the mushroom in the young, button stage. As the stem expands to raise the cap the universal veil is broken and a volva may be left as a remnant of the veil's lower part. Sometimes remnants remain on the cap as well and Amanita muscaria
.
Most mushroom genera have neither a ring nor a volva (with a volva being rarer
than a ring). Thus the possession of one (or both) of these features is of great
help in identification. Volva and ring are remnants of tissues that are present in the young stages of many mushrooms. A universal veil is a membrane that envelops the whole of the mushroom in the young, button stage. As the stem expands to raise the cap the universal veil is broken and a volva may be left as a remnant of the veil's lower part. Sometimes remnants remain on the cap as well and Amanita muscaria ![]() is an example of this. The white flecks on the red cap are remnants of a universal veil but such a veil doesn't always leave remnants on the cap. In a number of species the upper veil tissue is shed completely, leaving a smooth cap and an example is Volvariella speciosa
is an example of this. The white flecks on the red cap are remnants of a universal veil but such a veil doesn't always leave remnants on the cap. In a number of species the upper veil tissue is shed completely, leaving a smooth cap and an example is Volvariella speciosa ![]() , a species with a universal veil and a volva but with no veil remnants on the cap.. A partial veil covers the gills in a young mushroom. It extends from the stem to the edge of the cap and once the cap has fully expanded that veil breaks at the edge of the cap to expose the gills and the remnant hangs down around the stem as the ring. In this Amanita
, a species with a universal veil and a volva but with no veil remnants on the cap.. A partial veil covers the gills in a young mushroom. It extends from the stem to the edge of the cap and once the cap has fully expanded that veil breaks at the edge of the cap to expose the gills and the remnant hangs down around the stem as the ring. In this Amanita ![]() the partial veil was still intact when I turned the mushroom over but I have damaged the mushroom slightly to expose some of the gills. You can see that the partial veil is membranous whereas the partial veil shown in this photo
the partial veil was still intact when I turned the mushroom over but I have damaged the mushroom slightly to expose some of the gills. You can see that the partial veil is membranous whereas the partial veil shown in this photo ![]() is much flimsier, more like a thick cobweb and there are genera with even flimsier partial veils. Their are four possible combinations. A few genera possess both types of veil. There is also small number of genera with only a universal veil. A larger number of genera possess just a partial veil but most common is the absence of both veils.
is much flimsier, more like a thick cobweb and there are genera with even flimsier partial veils. Their are four possible combinations. A few genera possess both types of veil. There is also small number of genera with only a universal veil. A larger number of genera possess just a partial veil but most common is the absence of both veils.
Other types can also show considerable variation in shape. Consider the polypores.
You can have solid, woody bracket-like forms such as Ganoderma australe
![]() and almost paper thin, centrally-stemmed ones such as Microporus xanthopus
and almost paper thin, centrally-stemmed ones such as Microporus xanthopus
![]() .
You could break the latter between your fingers but you'd bruise your knuckles
severely if you punched the former. Moving away from three-dimensional fruiting
bodies, a polypore such as Macrohyporia dictyopora
.
You could break the latter between your fingers but you'd bruise your knuckles
severely if you punched the former. Moving away from three-dimensional fruiting
bodies, a polypore such as Macrohyporia dictyopora ![]() grows sheet-like fruiting bodies at the bases of tree trunks. While all polypores
have pores on the undersides of their fruiting bodies, the pores vary greatly
in shape and size. In the species of Pycnoporus
grows sheet-like fruiting bodies at the bases of tree trunks. While all polypores
have pores on the undersides of their fruiting bodies, the pores vary greatly
in shape and size. In the species of Pycnoporus ![]() the pores are more or less circular and each is around a fifth of a millimetre
in diameter
the pores are more or less circular and each is around a fifth of a millimetre
in diameter ![]() .
On the other hand, the pores of Hexagonia apiaria are markedly angular
and from 2 to 4 millimetres in longest dimension. Here's a photo
.
On the other hand, the pores of Hexagonia apiaria are markedly angular
and from 2 to 4 millimetres in longest dimension. Here's a photo ![]() of a fragment from a Pycnoporus fruiting body placed within a pore of
Hexagonia apiaria.
of a fragment from a Pycnoporus fruiting body placed within a pore of
Hexagonia apiaria.
While many corticioid fungi are flat and quite two-dimensional, others have
wrinkles ![]() ,
warts
,
warts ![]() or spines
or spines ![]() .
While the margins of many corticioid fungi are smooth there are also those which
are uneven, anything from slightly fury
.
While the margins of many corticioid fungi are smooth there are also those which
are uneven, anything from slightly fury ![]() to having pronounced cord-like bundles of hyphae extending well-beyond the margin
to having pronounced cord-like bundles of hyphae extending well-beyond the margin
![]() .
.
The fruiting body of Dacryobolus sudans ![]() is a flat sheet with numerous, crowded, creamy teeth, each about a half millimetre long. If you look with a hand lens you'll get a view much like this
is a flat sheet with numerous, crowded, creamy teeth, each about a half millimetre long. If you look with a hand lens you'll get a view much like this ![]() which shows a small, exuded droplet of viscous liquid at the apex of each tooth. In the wild the fruiting bodies form on the underside of rotten wood, so the teeth would be pointing down. The brownish spots on the gill edges
which shows a small, exuded droplet of viscous liquid at the apex of each tooth. In the wild the fruiting bodies form on the underside of rotten wood, so the teeth would be pointing down. The brownish spots on the gill edges ![]() of these mushrooms of Hebeloma crustuliniforme are dried droplets of exuded liquid.
of these mushrooms of Hebeloma crustuliniforme are dried droplets of exuded liquid.
Everyone would be aware of the multitude of colours that can be seen in the
fungal world. There can be considerable variation in colours between different
parts of the fruiting body – occasionally even in something like a mushroom
gill. This photo shows the underside of the cap of Pluteus atromarginatus
![]() . The gills are mostly white – but with a prominent black edge. In
most mushrooms the gill edge has the same colour as the rest of the gill, but
not always. It pays to look. Even when the gill edges are not so strikingly
coloured they may still be differentiated from the rest of the gill. In a number
of mushroom genera, the gill edges are lined with elongated colourless cells.
These give the gill edges a raggedy, hoary look as shown in this photo.
. The gills are mostly white – but with a prominent black edge. In
most mushrooms the gill edge has the same colour as the rest of the gill, but
not always. It pays to look. Even when the gill edges are not so strikingly
coloured they may still be differentiated from the rest of the gill. In a number
of mushroom genera, the gill edges are lined with elongated colourless cells.
These give the gill edges a raggedy, hoary look as shown in this photo. ![]()
While on the subject of gills, if you look at this photo that shows the underside
of a cap of Marasmius elegans ![]() ,
with the bulk of the stem removed, you’ll see that while many gills reach
the stem there are also minor gills which reach in only a little way from the
margin. This is typical for many mushrooms. However, there are also some mushroom
genera where even the main gills do not reach the stem. In this picture of an
Agaricus species
,
with the bulk of the stem removed, you’ll see that while many gills reach
the stem there are also minor gills which reach in only a little way from the
margin. This is typical for many mushrooms. However, there are also some mushroom
genera where even the main gills do not reach the stem. In this picture of an
Agaricus species ![]() you can see a prominent "gill-free" channel around the stem. So here’s
another feature – either the main gills reach the stem or they don’t.
If they do then they may be attached to the stem in various ways. The following
diagram shows some possibilities. Each represents a side-on view of one of the
main gills. It’s a stylised depiction of the sort of view you’d get
if you sliced a mushroom in half, vertically. The grey areas represent the flesh
of the cap and stem while the red areas show the gills. The first figure represents
the Agaricus situation, where the main gills do not reach the stem. The
arrow indicates the "gill-free" channel mentioned above. In the next
figure the gill does reach the stem, but only slightly. The other three figures
show some of the other possibilities. Finally, gills come in various shapes
– not just flat-bottomed as in the following diagram. The gills of mushrooms may be simple or they may fork as you can see here
you can see a prominent "gill-free" channel around the stem. So here’s
another feature – either the main gills reach the stem or they don’t.
If they do then they may be attached to the stem in various ways. The following
diagram shows some possibilities. Each represents a side-on view of one of the
main gills. It’s a stylised depiction of the sort of view you’d get
if you sliced a mushroom in half, vertically. The grey areas represent the flesh
of the cap and stem while the red areas show the gills. The first figure represents
the Agaricus situation, where the main gills do not reach the stem. The
arrow indicates the "gill-free" channel mentioned above. In the next
figure the gill does reach the stem, but only slightly. The other three figures
show some of the other possibilities. Finally, gills come in various shapes
– not just flat-bottomed as in the following diagram. The gills of mushrooms may be simple or they may fork as you can see here ![]() and here
and here ![]() . So even if you looked at just
the gills – there’s a lot to be seen.
. So even if you looked at just
the gills – there’s a lot to be seen.

Spore colour, as shown in a spore print, is very useful. The colour of the
spore print is often different to gill colour. If you’re not familiar with
spore prints see the SPORE
PRINT SECTION. Sometimes spore colour shows easily in the field. In this photograph ![]() you can see that a lot of pinkish brown spores have fallen from the upper cap onto the lower. You can also easily see the colour of massed spores in various
powdery-spored fruiting bodies. Contrast the lilaceous spore mass of Calvatia
lilacina
you can see that a lot of pinkish brown spores have fallen from the upper cap onto the lower. You can also easily see the colour of massed spores in various
powdery-spored fruiting bodies. Contrast the lilaceous spore mass of Calvatia
lilacina ![]() with the brown of Scleroderma
with the brown of Scleroderma ![]() .
.
Apart from the ordinary colours of the fruiting bodies themselves, there are
sometimes changes in colour when the fruiting body is damaged. For example,
if you run your fingernail across the white underside of the polypore Amauroderma
rude, you'll see a red line appear, as shown in the photograph (right).
In various boletes the inside flesh will turn blue when exposed to air ![]() .
.
Continuing with the theme of damage, species in the mushroom genus Lactarius
will ooze a liquid when damaged. In this photo (left) you can see a small white
drop of fluid on the gills, where a fingernail has been pressed into them. You
can also see a similar drop of fluid on the exposed flesh of this truffle-like
fungus, in the genus Zelleromyces ![]() .
Such colour changes, or bleeding, are not too common.
.
Such colour changes, or bleeding, are not too common.
Fruiting bodies may be anything from dry to sticky. For example, this Hygrocybe
![]() is exceedingly sticky. You can see a slippery, gelatinous layer over both the
stem and the cap. In some sticky mushroom species the stickiness isn’t
everywhere, (e.g. the cap may be sticky – but the stem dry as is the case with Suillus luteus
is exceedingly sticky. You can see a slippery, gelatinous layer over both the
stem and the cap. In some sticky mushroom species the stickiness isn’t
everywhere, (e.g. the cap may be sticky – but the stem dry as is the case with Suillus luteus ![]() ).
).
Some mushrooms have strongly pleated caps. ![]()
If there’s a cap, is it smooth or rough (and how rough) on the upper side?
The upper surface of the polypore Hexagonia apiaria is covered with very
stiff, branched hairs ![]() . Smoothness and roughness can help differentiate non-capped fungi as well. Species of Geoglossum
. Smoothness and roughness can help differentiate non-capped fungi as well. Species of Geoglossum ![]() have smooth, black fruiting bodies while the similarly-shaped black fruiting bodies of Trichoglossum
have smooth, black fruiting bodies while the similarly-shaped black fruiting bodies of Trichoglossum ![]() are densely covered with short bristles.
are densely covered with short bristles.
The upper surface of Trametes versicolor ![]() (another polypore) is covered in very short hairs, giving a velvety feel. The
margin of the ascomycete Jafneadelphus ferrugineus
(another polypore) is covered in very short hairs, giving a velvety feel. The
margin of the ascomycete Jafneadelphus ferrugineus ![]() has a slight roughness while there are easily visible hairs around the disk
of Scutellinia
has a slight roughness while there are easily visible hairs around the disk
of Scutellinia ![]() .
The red cap of Amanita muscaria
.
The red cap of Amanita muscaria ![]() ,
while generally smooth, has small pieces of white tissue stuck to the cap. The
cap of Leucocoprinus birnbaumii
,
while generally smooth, has small pieces of white tissue stuck to the cap. The
cap of Leucocoprinus birnbaumii ![]() has a fine, granular coating – the granules being easily rubbed off.
has a fine, granular coating – the granules being easily rubbed off.
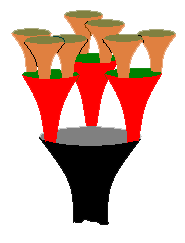 Coral
fungi show different types of branching. Some branch in much the same way as
trees, with a main trunk dividing smoothly into two or more, those later dividing
smoothly again and so on. A more dramatic type of branching is what’s called
pyxidate branching. Here, one level finishes in a disk-like to cup-like
area and the branches for the next level start at the margins of the disk or
cup. The diagram shows this in stylized form and the photo shows a close-up
view of a species of Clavicorona
Coral
fungi show different types of branching. Some branch in much the same way as
trees, with a main trunk dividing smoothly into two or more, those later dividing
smoothly again and so on. A more dramatic type of branching is what’s called
pyxidate branching. Here, one level finishes in a disk-like to cup-like
area and the branches for the next level start at the margins of the disk or
cup. The diagram shows this in stylized form and the photo shows a close-up
view of a species of Clavicorona ![]() where you can see some very young branches developing around the rim of one
of these disk-like areas.
where you can see some very young branches developing around the rim of one
of these disk-like areas.
A number of puffballs (and their close relatives) are simply bags of spores,
but that’s not the case for all of these fungi. There may be a spongy base
that holds up the spore-filled part, especially where the fruiting body is elongated,
as in this photo. In this specimen the rounded upper part holds the spores while
the cylindrical lower part is simply a supporting base .
|
Calvatia sp. photo right Illustration above shows two genera with similar form. |
 |
The spongy base has numerous air-chambers and looks a bit like solidified foam. If there is a spongy base there are two further possibilities: either there’s a definite membrane between the spongy base and the spore-filled upper section, or there isn’t. In the diagram, the spongy base is shown in greyish blue, the spores in brown and (on the right) there’s a red membrane.
While on the subject of puffballs, the skin of the spore sack often has a roughened
surface when young. With age, much of that roughened surface may disappear –
or be retained only on the lower half of the puffball. A close look at a number
of puffball species shows a variety of causes of such roughness – e.g.
simple granules, conical spines, groups of spines joined at their apices, as
shown in the photo ![]() .
.
An Earthstar (the genus Geastrum ![]() )
looks like a puffball on a star-like base. The spore sack may sit directly on
the star-like base or be raised on a short stalk. The apical opening through
which the spores are released may be a fairly simple affair
)
looks like a puffball on a star-like base. The spore sack may sit directly on
the star-like base or be raised on a short stalk. The apical opening through
which the spores are released may be a fairly simple affair ![]() or more complex, such as the conical, pleated structure on Geastrum pectinatum
or more complex, such as the conical, pleated structure on Geastrum pectinatum
![]() .
.
While the bulk of the fungi that produce spore-sacs on star-like bases are
in the genus Geastrum, not all of them are. Look carefully and you may
come across Myriostoma coliforme ![]() .
While a Geastrum fruiting body has just one apical spore-releasing pore,
in Myriostoma coliforme there are several.
.
While a Geastrum fruiting body has just one apical spore-releasing pore,
in Myriostoma coliforme there are several.
Does the fruiting body have a distinctive smell (other than ‘mushroomy’!). Is it fruity, cucumber-like, radish-like, nauseous, like stale urine, strongly reminiscent of rotten meat, musky, like marzipan? All occur in fungi.
Where are the fruiting bodies growing – in a eucalypt forest, a pine plantation, the middle of a sheep paddock or in the arid inland? On the seashore or in the alps?
What is the fruiting body growing from – wood, soil, dung (e.g. Cyathus
stercoreus ![]() ) or (like many species of Cordyceps
) or (like many species of Cordyceps ![]() from insect larvae or pupae?
from insect larvae or pupae?
If it's a wood-rotting fungus - does it cause a brown rot or a white rot? White
rot ![]() leaves the wood bleached and with a stringy consistency. Brown rot
leaves the wood bleached and with a stringy consistency. Brown rot ![]() leaves the wood coloured brown and typically with extensive cracking into small
and more or less cubical sections.
leaves the wood coloured brown and typically with extensive cracking into small
and more or less cubical sections.
What is its texture – gelatinous (like Tremella fuciformis ![]() ) fleshy, leathery or woody?
) fleshy, leathery or woody?
 Do
the fruiting bodies grow in dense clusters or isolated from each other?
Do
the fruiting bodies grow in dense clusters or isolated from each other?
This drawing, by Jim Willis (from his small book Victorian Toadstools and
Mushrooms) shows a small cluster of Marasmius elegans ![]() ,
with all the stems coming from a common point. A number of species characteristically
grow in this fashion, with some species forming quite large clusters. This type
of growth is not restricted to mushrooms. For example, some polypores also produce
bracket-like fruiting bodies in dense clusters, as shown by the following photo
,
with all the stems coming from a common point. A number of species characteristically
grow in this fashion, with some species forming quite large clusters. This type
of growth is not restricted to mushrooms. For example, some polypores also produce
bracket-like fruiting bodies in dense clusters, as shown by the following photo
![]() .
.
In both the drawing and photograph of Marasmius elegans you'll have
seen that there are short, hairy tufts at the bases of the stems. You'll find
such tufts at the bases of a number of mushrooms growing out of wood or forest
litter. On the other hand, Mycena interrupta ![]() has a small circular pad around the base of each stem. There are also many mushrooms
which have no tufts or pads, but have the stems coming cleanly out of the wood.
has a small circular pad around the base of each stem. There are also many mushrooms
which have no tufts or pads, but have the stems coming cleanly out of the wood.
Does the fruiting body glow in the dark, as is the case with Omphalotus
nidiformis? ![]() .
.
Are sclerotia present? Sclerotia are compacted masses of hyphae, used by some
fungi as dormant bodies which will produce a fresh mycelium or fruiting bodies
when good conditions return. This is the sclerotium of Laccocephalum mylittae
![]() and the other photos show a sclerotium of Hypholoma tuberosum as well
as a mushroom growing from such a sclerotium
and the other photos show a sclerotium of Hypholoma tuberosum as well
as a mushroom growing from such a sclerotium
 |
If it's a wood-rotting fungus, does the mycelium colour the wood? For example,
the mycelium of Chlorociboria aeruginascens ![]() gives an aqua colour to the underlying wood
gives an aqua colour to the underlying wood ![]() .
Amongst the wood-inhabiting ascomycetes are a number of genera in which apothecia develop within the wood, the mature apothecia being exposed by shedding the outer layer of wood or bark. Propolomyces versicolor
.
Amongst the wood-inhabiting ascomycetes are a number of genera in which apothecia develop within the wood, the mature apothecia being exposed by shedding the outer layer of wood or bark. Propolomyces versicolor ![]() is an example of such a species and the largest of apothecia in that photo is about a half centimetre in diameter. You can see torn edges of host tissue around the exposed white apothecial surfaces. Stictis
is an example of such a species and the largest of apothecia in that photo is about a half centimetre in diameter. You can see torn edges of host tissue around the exposed white apothecial surfaces. Stictis ![]() < is another genus with immersed apothecia, each no more than about a millimetre in diameter.
< is another genus with immersed apothecia, each no more than about a millimetre in diameter.
....... and the list of macroscopic features goes on and on. You'll find more in the references given earlier as well as many of the basic fungal books you'll find in libraries.
So the next time you see a mushroom, puffball, bracket fungus or any other fungal fruiting body – take your time and study it in detail. You can learn a lot by using your eyes and a magnifying glass.